SISTEMAS DE CONTROLE I
Um sistema de controle apresenta o seguinte diagrama de polos e zeros:
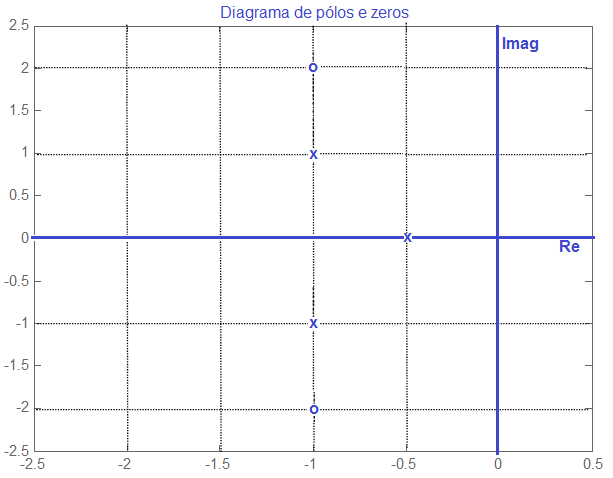
Sua função de transferência é:





Um sistema de primeira ordem, com função de transferência F(s), recebe excitação de entrada do tipo degrau de amplitude 10, e apresenta resposta c(t) dada no gráfico abaixo.
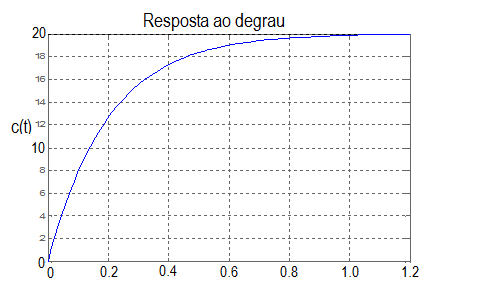
Dentre as opções apresentadas abaixo, qual melhor representa a função de transferência F(s) e a resposta ao degrau c(t)? (considere exp - exponencial de base e)
F(s)=2/(s + 1) e c(t)=20.(1-exp(-t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
F(s)=20/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=10/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
A figura apresenta o esquema elétrico de um sistema com amplificadores operacionais , e sua representação por diagramas de blocos e funções de transferência.
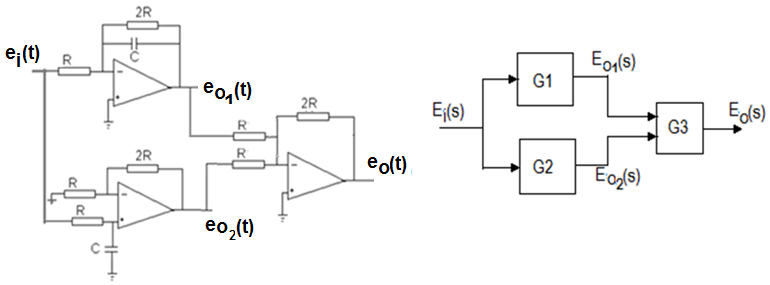
Analise as informações contidas nas afirmativas seguintes:
I. Eo1(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a -2 e pólo igual a -1/(2RC).
II. Eo2(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a 3 e pólo igual a -1/(RC).
III. Eo(s)/Ei(s) é função de transferência de segunda ordem, com ganho igual a -2, e pólos iguais a -1/(2RC) e -1/(RC)
IV. G2 = 3/(R.C.s+1)
V. G1 = 2/(2.R.C.s+1)
VI. G3 é um bloco subtrator com ganho 2
VII. Eo(s)=( G1+G2).G3.Ei(s)
VIII. Se ei(t)=1 V, em regime permanente, eo(t)= -1 V
As afirmativas verdadeiras são:
II, IV, VI, VII
I, II, III, IV, VII
II, III, IV, VI, VII
I, II, III, IV, VI, VII
I, II, V, VI, VII
Um sistema físico tem como entrada a variável r(t), e como saída a variável y(t).
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7B3%7D.%5Cfrac%7B%7B%7B%5Cleft.%7Bd%7D%7By%7D%5Cright.%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%5Cfrac%7B%7B%7Bd%7D%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
A função de transferência Y(s)/R(s), portanto, será:
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B1%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BY%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
Considere os polinômios abaixo, onde s é a variável do domínio da frequência, atrelada às transformadas de Laplace:
num(s)=s+1
den(s)=s2+s+1
Se a função de transferência FT(s) de um determinado sistema é dada pela razão: FT(s)=num(s)/den(s), analise as afirmativas:
I - O sistema tem dois pólos (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um zero (z=-1).
II - O ganho do sistema é unitário
III - O sistema tem dois zeros (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um polo (z=-1).
IV - O ganho do sistema é zero
V - O sistema tem dois zeros (z1=-0,5-j.0,87 e z2=-0,5+j.0,87) e não possui pólos.
São corretas as afirmativas:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:

Um sistema de primeira ordem, com função de transferência F(s), recebe excitação de entrada do tipo degrau de amplitude 10, e apresenta resposta c(t) dada no gráfico abaixo.

Dentre as opções apresentadas abaixo, qual melhor representa a função de transferência F(s) e a resposta ao degrau c(t)? (considere exp - exponencial de base e)
F(s)=2/(s + 1) e c(t)=20.(1-exp(-t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
F(s)=20/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=10/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
A figura apresenta o esquema elétrico de um sistema com amplificadores operacionais , e sua representação por diagramas de blocos e funções de transferência.

Analise as informações contidas nas afirmativas seguintes:
I. Eo1(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a -2 e pólo igual a -1/(2RC).
II. Eo2(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a 3 e pólo igual a -1/(RC).
III. Eo(s)/Ei(s) é função de transferência de segunda ordem, com ganho igual a -2, e pólos iguais a -1/(2RC) e -1/(RC)
IV. G2 = 3/(R.C.s+1)
V. G1 = 2/(2.R.C.s+1)
VI. G3 é um bloco subtrator com ganho 2
VII. Eo(s)=( G1+G2).G3.Ei(s)
VIII. Se ei(t)=1 V, em regime permanente, eo(t)= -1 V
As afirmativas verdadeiras são:
II, IV, VI, VII
I, II, III, IV, VII
II, III, IV, VI, VII
I, II, III, IV, VI, VII
I, II, V, VI, VII
Um sistema físico tem como entrada a variável r(t), e como saída a variável y(t).
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7B3%7D.%5Cfrac%7B%7B%7B%5Cleft.%7Bd%7D%7By%7D%5Cright.%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%5Cfrac%7B%7B%7Bd%7D%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
A função de transferência Y(s)/R(s), portanto, será:
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B1%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BY%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
Considere os polinômios abaixo, onde s é a variável do domínio da frequência, atrelada às transformadas de Laplace:
num(s)=s+1
den(s)=s2+s+1
Se a função de transferência FT(s) de um determinado sistema é dada pela razão: FT(s)=num(s)/den(s), analise as afirmativas:
I - O sistema tem dois pólos (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um zero (z=-1).
II - O ganho do sistema é unitário
III - O sistema tem dois zeros (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um polo (z=-1).
IV - O ganho do sistema é zero
V - O sistema tem dois zeros (z1=-0,5-j.0,87 e z2=-0,5+j.0,87) e não possui pólos.
São corretas as afirmativas:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:

F(s)=2/(s + 1) e c(t)=20.(1-exp(-t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
F(s)=20/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=2/(0,2 s + 1) e c(t)=20.(1-exp(-5.t))
F(s)=10/(0,2 s + 1) e c(t)=20.(1-exp(-0,2.t))
A figura apresenta o esquema elétrico de um sistema com amplificadores operacionais , e sua representação por diagramas de blocos e funções de transferência.

Analise as informações contidas nas afirmativas seguintes:
I. Eo1(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a -2 e pólo igual a -1/(2RC).
II. Eo2(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a 3 e pólo igual a -1/(RC).
III. Eo(s)/Ei(s) é função de transferência de segunda ordem, com ganho igual a -2, e pólos iguais a -1/(2RC) e -1/(RC)
IV. G2 = 3/(R.C.s+1)
V. G1 = 2/(2.R.C.s+1)
VI. G3 é um bloco subtrator com ganho 2
VII. Eo(s)=( G1+G2).G3.Ei(s)
VIII. Se ei(t)=1 V, em regime permanente, eo(t)= -1 V
As afirmativas verdadeiras são:
II, IV, VI, VII
I, II, III, IV, VII
II, III, IV, VI, VII
I, II, III, IV, VI, VII
I, II, V, VI, VII
Um sistema físico tem como entrada a variável r(t), e como saída a variável y(t).
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7B3%7D.%5Cfrac%7B%7B%7B%5Cleft.%7Bd%7D%7By%7D%5Cright.%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%5Cfrac%7B%7B%7Bd%7D%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
A função de transferência Y(s)/R(s), portanto, será:
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B1%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BY%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
Considere os polinômios abaixo, onde s é a variável do domínio da frequência, atrelada às transformadas de Laplace:
num(s)=s+1
den(s)=s2+s+1
Se a função de transferência FT(s) de um determinado sistema é dada pela razão: FT(s)=num(s)/den(s), analise as afirmativas:
I - O sistema tem dois pólos (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um zero (z=-1).
II - O ganho do sistema é unitário
III - O sistema tem dois zeros (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um polo (z=-1).
IV - O ganho do sistema é zero
V - O sistema tem dois zeros (z1=-0,5-j.0,87 e z2=-0,5+j.0,87) e não possui pólos.
São corretas as afirmativas:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:

II, IV, VI, VII
I, II, III, IV, VII
II, III, IV, VI, VII
I, II, III, IV, VI, VII
I, II, V, VI, VII
Um sistema físico tem como entrada a variável r(t), e como saída a variável y(t).
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7B3%7D.%5Cfrac%7B%7B%7B%5Cleft.%7Bd%7D%7By%7D%5Cright.%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%5Cfrac%7B%7B%7Bd%7D%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7B2%7D.%7Br%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
A função de transferência Y(s)/R(s), portanto, será:
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B1%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BY%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
%7D%7D%7D%7B%7B%7BR%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D.%7Bs%7D%2B%7B2%7D%7D%7D)
Considere os polinômios abaixo, onde s é a variável do domínio da frequência, atrelada às transformadas de Laplace:
num(s)=s+1
den(s)=s2+s+1
Se a função de transferência FT(s) de um determinado sistema é dada pela razão: FT(s)=num(s)/den(s), analise as afirmativas:
I - O sistema tem dois pólos (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um zero (z=-1).
II - O ganho do sistema é unitário
III - O sistema tem dois zeros (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um polo (z=-1).
IV - O ganho do sistema é zero
V - O sistema tem dois zeros (z1=-0,5-j.0,87 e z2=-0,5+j.0,87) e não possui pólos.
São corretas as afirmativas:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:
Considere os polinômios abaixo, onde s é a variável do domínio da frequência, atrelada às transformadas de Laplace:
num(s)=s+1
den(s)=s2+s+1
Se a função de transferência FT(s) de um determinado sistema é dada pela razão: FT(s)=num(s)/den(s), analise as afirmativas:
I - O sistema tem dois pólos (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um zero (z=-1).
II - O ganho do sistema é unitário
III - O sistema tem dois zeros (p1=-0,5-j.0,87 e p2=-0,5+j.0,87) e um polo (z=-1).
IV - O ganho do sistema é zero
V - O sistema tem dois zeros (z1=-0,5-j.0,87 e z2=-0,5+j.0,87) e não possui pólos.
São corretas as afirmativas:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:
IV e V
I e III
III e IV
II e III
I e II
A transformada de Laplace inversa da função
%7D%3D%7B4%7D.%5Cfrac%7B%7B%7Bs%7D%2B%7B5%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B5%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D-%5Cfrac%7B%7B6%7D%7D%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B5%7D%7D%7B%7B%7Bs%7D-%7B4%7D%7D%7D)
é a função f(t) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é:
f (t) = 4.e5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t3 + 5e4t.
f (t) = 4.e5t cos(2t) - 3t2 + 5e4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e-4t.
f (t) = 4.e-5t cos(2t) - 3t2 + 5e4t.
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
%7D%5Cright)%7D%7D%7D%7B%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%5Cright.%7D%7D%5E%7B%7B2%7D%7D%7D%2B%7Bb%7D.%5Cfrac%7B%7B%7Bd%7D%7B%5Cleft(%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%5Cright)%7D%7D%7D%7B%7B%5Cleft.%7Bd%7D%7Bt%7D%7D%7D%2B%7Bc%7D.%7By%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D%3D%7Bk%7D.%7Bu%7D%7B%5Cleft(%7Bt%7D%5Cright)%7D)
Sendo k=1, a=1, b=3 e c=2. Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t), relativa à variação da posição do braço, será:
%7D%3D)

%7D%3D)

%7D%3D%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B%7Bt%7D%7D%7D%7D%2B%5Cfrac%7B%7B1%7D%7D%7B%7B2%7D%7D.%7B%7Be%7D%7D%5E%7B%7B-%7B2%7D%7Bt%7D%7D%7D)
%7D%3D)
%7D%7D%7D%7D-%7B%7Be%7D%7D%5E%7B%7B-%7B3%7D%7Bt%7D%7D%7D)
%7D%3D)

Avalie as afirmativas seguintes, relativas aos gráficos do lugar das raízes:
1) É o lugar geométrico do plano s que contém todos os possíveis polos de um sistema de malha fechada, considerando a variação de um parâmetro na função de transferência de malha fechada.
2) O lugar das raízes começa com valor de K=0 (nos pólos , ou raízes de denec) , e termina com K=∞ (nos zeros finitos ( raizes de numec), ou no infinito, caso não existam zeros finitos), onde K é o parâmetro variável da função de transferência do sistema.
3) Apenas os pólos mudam de posição no gráfico do lugar das raízes, os zeros não mudam de valor.
4) A trajetória descrita pelos pólos, à medida que K varia é chamada de ramo.
5) O número de ramos é sempre igual ao número de pólos.
6) O ponto onde dois ou mais ramos se encontram é chamado ponto de ramificação.
7) Um segmento específico do eixo real irá pertencer ao lugar das raízes se o número de pólos e zeros à esquerda desse segmento for ímpar.
8) O lugar das raízes é simétrico em relação ao eixo imaginário.
9) sistemas estáveis possuem todos os pólos à esquerda do eixo imaginário , enquanto que sistemas instáveis têm um ou mais pólos à direita do eixo imaginário do plano s
10) No limite da estabilidade, existirão pares de pólos estão sobre o eixo real
A quantidade de afirmativas da relação que são verdadeiras é: